Distance between two cities along the great circle connecting them.

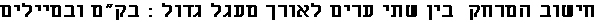
The distance was calculated using the cosine equation for the spherical triangle P(North-Pole),A,B:

Distace = Earth-Radius * (arccos ( cos(90-a)*cos(90-b) + sin(90-a)*sin(90-b)*cos(P1-P2) ) ), - or

Distace = Earth-Radius * (arccos ( sin(a)*sin(b) + cos(a)*cos(b)*cos(P1-P2) ) )

---

EXAMPLE

Latitude of Jerusalem: 31.75

Longtitude of Jerusalem: 35.25

Latitude of Los Angeles: 34.0

Longtitude of Los Angeles: -118.0

Click on the button "calculate"

and the calculated distance between the cities of Jerusalem and Los Angeles turns out to be 12,185 km; or, 7573 miles; or 6579 nautical miles.

In order to find the coordinates of other cities here.

 Return to the Main Page.

---

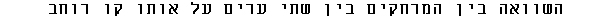
Comparison of the distances between two cities located on the same latitude a , once along the great circle connecting them, calculated as above, and once along their common latitude , calculated using the equation:

Distance along the common latitude = [111.1 * (P2-P1) * cos(a)] km.

Latitude of city A	= a, (minus sign for Southern Latitudes.)
Longtitude of city A	= P1, (minus sign for Western Longitudes.)

---

Longtitude of city B

= P2.

---

The distance between the cities A and B is km along the great circle; and km along the latitude connecting them.